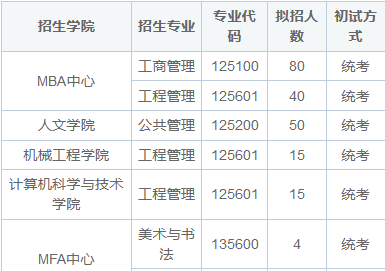
2024年东华大学非全日制研究生招生考试《统计学》考试大纲
一、考查目标
全国硕士研究生招生统一考试应用统计硕士专业学位《统计学》考试是为高等院校和科研院所招收应用统计硕士生而设置的具有选拔性质的考试科目。
其目的是科学、公平、有效地测试考生是否具备攻读应用统计专业硕士所必须的基本素质、一般能力和培养潜能,以利用选拔具有发展潜力的优秀人才入学,为国家的经济建设培养具有良好职业道德、法制观念和国际视野、具有较强分析与解决实际问题能力的高层次、应用型、复合型的统计专业人才。考试要求是测试考生掌握统计学的基础理论知识和基本技能。具体来说。
要求考生:
1.理解统计学的基本概念;
2.具有分析数据和解释数据的基本能力。
3.具有扎实的概率论基础;
4.掌握推断统计学的基本原理和方法。
二、考试形式和试卷结构
1.试卷满分及考试时间
试卷满分为150分,考试时间180分钟。
2.答题方式
答题方式为闭卷、笔试。允许使用计算器,但不得使用带有公式和文本存储功能的计算器。
3.试卷内容与题型结构
单项选择题 20题,每小题2分,共40分
简答题 5题,每小题10分,共50分
计算与分析题 6题,每小题10分,共60分
三、考查内容(*含网上资料内容)
统计抽样;
数据的预处理;
用图和表展示数据;
用统计量描述数据的水平:均值、中位数、四分位数、分位数和众数;
用统计量描述数据的差异:极差、样本方差、样本标准差;
样本协方差与样本相关系数;
*Excel描述统计。
事件的关系和运算;
概率的定义与性质;
古典概型与几何概型;
条件概率、乘法公式、全概率公式和贝叶斯公式;
事件的独立性。
随机变量和分布函数;
离散型随机变量的分布律和分布函数;
连续型随机变量的概率密度函数和分布函数;
多维离散型随机变量的联合分布律、边缘分布率、条件分布律;
*多维随机变量的联合分布函数和边缘分布函数;
*多维连续型随机变量的联合密度函数、边缘密度函数、条件密度函数;
*随机变量函数的分布;
随机变量的独立性;
随机变量的期望与方差;
随机变量函数的期望;期望和方差的性质;
切比雪夫不等式;
协方差与相关系数。
伯努利分布、二项分布、泊松分布;
*几何分布与超几何分布;
均匀分布、指数分布、正态分布;
*二维均匀分布与二维正态分布;
卡方分布、t分布和F分布;
*Excel概率分布和分位数计算。
简单随机抽样;
正态总体的抽样定理;
辛钦大数定律与伯努利大数定律;
蒙特卡罗算法;
*Excel实现蒙特卡罗算法;
中心极限定理,二项分布的正态近似;
*离散变量的连续修正;
大样本均值的近似分布。
点估计的概念;
*矩估计法;
估计量的性质;
最大似然估计;
置信区间的概念;
一个总体均值的区间估计;
*一个正态总体方差的区间估计;
*两个正态总体参数的区间估计;
样本量的确定。
假设检验的基本原理;
统计推断中的两类错误;
临界值判别法与p值判别法;
一个总体均值的假设检验;
*成对样本均值差的假设检验;
*一个正态总体方差的假设检验;
*两个正态总体参数的假设检验。一元线性回归模型;
回归模型的方差分析和假设检验;
回归模型的参数估计;
回归预测。
报考资格评估
- 大专以下
- 大专
- 本科有学位
- 本科无学位
- 硕士
- 博士