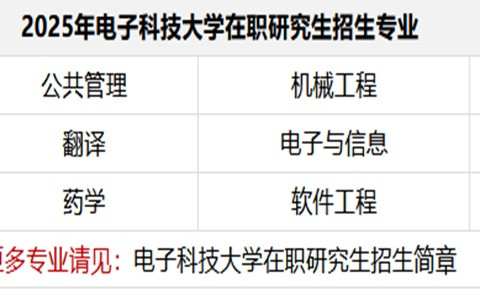
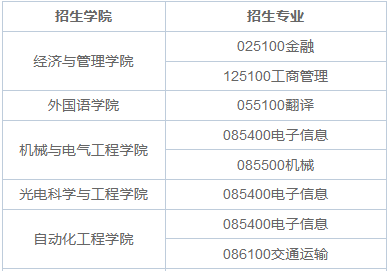
2024年电子科技大学非全日制研究生招生考试《单独考试高等数学》考试大纲
一、总体要求
主要考察考生的基本数学素质。理解高等数学的基本概念与基本理论;掌握高等数学的基本方法 与基本技能;并运用高等数学的概念、理论与方法解决一些简单的实际问题。
二、内容
1. 函数、极限、连续
1) 函数的概念及表示法 、函数的有界性、单调性、周期性和奇偶性;
2) 复合函数、反函数、分段函数和隐函数 、 基本初等函数的性质及其图形、 初等函数、 函数关系的建立;
3) 数列极限与函数极限的定义及其性质,函数的左极限和右极限,无穷小量和无穷大量的概 念及其关系,无穷小量的性质及无穷小量的比较;
4) 极限的四则运算,极限存在的两个准则,单调有界准则和夹逼准则,两个重要极限, 函数连续的概念,函数间断点的类型,初等函数的连续性, 闭区间上连续函数的性质。
2. 一元函数微分学
1) 导数和微分的概念,导数的几何意义和物理意义;
2) 函数的可导性与连续性之间的关系,平面曲线的切线和法线;
3) 导数和微分的四则运算 ;
4) 基本初等函数的导数、复合函数、反函数、隐函数以及参数方程所确定的函数的微分法, 高阶导数 、一阶微分形式的不变性;
5) 微分中值定理 、 洛必达(L’Hospital)法则、函数单调性的判别、 函数的极值、函数图形的凹凸性、拐点及渐近线、函数图形。
3. 一元函数积分学
1) 原函数和不定积分的概念,不定积分的基本性质,基本积分公式, 定积分的概念和基本性质 ;
2) 定积分中值定理、 积分上限的函数及其导数、 牛顿-莱布尼茨(Newton-Leibniz)公式;
3) 不定积分和定积分的换元积分法与分部积分法;
4) 有理函数、三角函数的有理式和简单无理函数的积分,反常(广义)积分 定积分的应用。
4. 向量代数和空间解析几何
1) 向量的概念、 向量的线性运算、向量的数量积和向量积、向量的混合积、两向量垂直、平行的条件、两向量的夹角、 向量的坐标表达式及其运算;
2) 单位向量、方向数与方向余弦、 曲面方程和空间曲线方程的概念;
3) 平面方程、直线方程、平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条 件、 点到平面和点到直线的距离;
4) 球面、柱面、旋转曲面、 常用的二次曲面方程及其图形、空间曲线的参数方程和一般方程、 空间曲线在坐标面上的投影曲线方程。
5. 多元函数微分学
1) 多元函数的概念、 二次函数的几何意义, 二元函数的极限与连续的概念
2) 有界闭区域上多元连续函数的性质, 多元函数的偏导数和全微分,全微分存在的必要条件和充分条件;
3) 多元复合函数、隐函数的求导法, 二阶偏导数、方向导数和梯度、空间曲线的切线和法平面、 曲面的切平面和法线 ;
4) 多元函数的极值和条件极值 多元函数的最大值、最小值及其简单应用。
6. 多元函数积分学
1) 二重积分与三重积分的概念、性质、计算和应用;
2) 两类曲线积分的概念、性质及计算、 两类曲线积分的关系,格林(Green)公式,平面曲线积分与路径无关的条件;
3) 二元函数全微分的原函数, 两类曲面积分的概念、性质及计算, 两类曲面积分的关系;
4) 高斯(Gauss)公式、斯托克斯(Stokes)公式、散度、旋度的概念及计算;
5) 曲线积分和曲面积分的应用。
7. 无穷级数
1) 常数项级数的收敛与发散的概念,收敛级数的和的概念,级数的基本性质与收敛的必要条 件,几何级数与 p 级数及其收敛性;
2) 正项级数收敛性的判别法,交错级数与莱布尼茨定理,任意项级数的绝对收敛与条件收敛 函数项级数的收敛域与和函数的概念;
3) 幂级数及其收敛半径、收敛区间(指开区间)和收敛域,幂级数的和函数,幂级数在其收 敛区间内的基本性质;
4) 简单幂级数的和函数的求法,初等函数的幂级数展开式,函数的傅里叶(Fourier)系数 与傅里叶级数,狄利克雷(Dirichlet)定理, 函数在[-p,p],[-l,l] 上的傅里叶级数, 函数在[0,p],[0,l] 上的正弦级数和余弦级数。
8. 常微分方程
1) 常微分方程的基本概念;
2) 变量可分离的微分方程、齐次微分方程、一阶线性微分方程、伯努利(Bernoulli)方程、 全微分方程、可降阶的高阶微分方程、线性微分方程解的性质及解的结构定理;
3) 二阶常系数齐次线性微分方程,高于二阶的某些常系数齐次线性微分方程,简单的二阶常 系数非齐次线性微分方程 欧拉(Euler)方程 微分方程的简单应用。
报考资格评估
- 大专以下
- 大专
- 本科有学位
- 本科无学位
- 硕士
- 博士